L’idea di un ordine armonico del cosmo è stata fonte di ispirazione per la storia del pensiero umano per migliaia di anni. Pitagora, che, secondo la leggenda, era in grado di sentire la ”musica delle sfere”, scoprí che gli intervalli musicali armonici possono essere espressi in intervalli di numeri interi piccoli. Platone trasferí questo concetto in un modello della struttura dell’universo che divenne fondamentale nel mondo antico. All’inizio dell’era scientifica, Giovanni Keplero diede un nuovo impeto alle idee antiche, che erano state guidate solo dall’intuizione. Keplero pose i fondamenti della moderna concezione dell’armonia delle sfere. Con l’ausilio delle leggi planetarie che aveva scoperto, Keplero cercó di dare un nuovo e solido fondamento alle idee antiche. La musica celeste, che Keplero cercó di trovare, era per lui solo ”percepibile nella mente”, e cioè egli cercò di trovare un parallelo tra gli intervalli musicali e le relazioni planetarie.

Giovanni Keplero
Fondation St. Thomas, Straßburg
Alla fine, Keplero pensó di averlo trovato nelle velocità angolari estreme dei pianeti (secondo Keplero queste sono date dagli spazi angolari, avendo come punto di osservazione il Sole, che i pianeti percorrono in intervalli di tempo uguali quando sono più lontani o più vicini al Sole).Altri ricercatori, dopo Keplero, si sono concentrati su altri parametri, che soddisferebbero le condizioni menzionate. Per esempio, Hans Kayser sviluppó una scala musicale planetaria dai logaritmi delle distanze, Thomas Michael Schmidt fece lo stesso basandosi sui periodi di rotazione sinodici (relativi alla terra) – e altri ancora. Manca invece del tutto, nella letteratura scientifica, uno studio sulla possibilità che le concordanze riscontrate siano significanti dal punto di vista del calcolo probabilistico. In altre parole, bisogna chiedersi se e in che misura le armonie planetarie ipotizzate differiscono da una distribuzione casuale. Quindi, in una serie di rapporti numerici, che possono essere derivati da fattori come la distanza, la velocità ecc., se ne troveranno sempre alcuni che si avvicinano agli intervalli musicali quali 2:1, 3:2, ecc.. Per evitare una lunga spiegazione matematica un semplice grafico illustra il concetto.
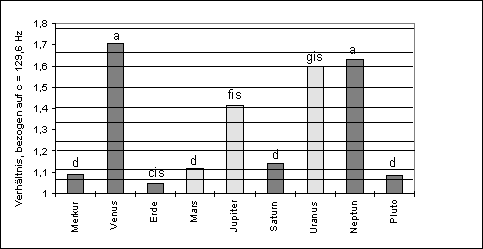
Figura 1.1
L’illustrazione 1.1 mostra le frequenze – trasposte in una singola ottava – derivate dai valori reciproci dei periodi di rivoluzione (le note di una ”scala musicale planetaria” secondo Hans Cousto). Le linee orizzontali mostrano gli intervalli musicali, ed è ovvio che solo 3 dei 9 valori planetari si avvicinano a quelli delle note musicali. Anche senza ulteriori calcoli, possiamo vedere che non c’è deviazione da una distribuzione casuale. Analizzando le altre armonie celesti sopra menzionate i risultati non sono più favorevoli, nemmeno con i valori angolari usati da Keplero. Ma Keplero è giustificato per aver fallito nell’elaborazione della sua idea di base, in quanto il calcolo probabilistico non era conosciuto ai suoi tempi. Inoltre, Keplero nel suo libro ”De Harmonice mundi” incoraggió esplicitamente il lettore a creare ”un sistema più adeguato ai movimenti celesti” del suo proprio.
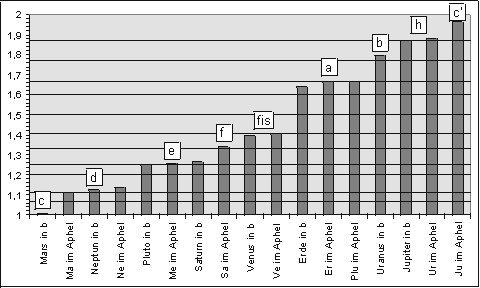
Figura 1.2
In questo modo troviamo che 13 su 17 possibili valori sono vicini o molto vicini agli intervalli musicali. Se usiamo il metodo di calcolo statistico, questo risultato può apparire solo con una probabilità di 1:10.000. Se prendiamo in considerazione il fatto che ci sono circa 10 possibilità di calcolare delle relazioni fra i diversi parametri menzionati, la probabilità risultante è ancora di 1:1000. Di conseguenza l’antica idea di una ”armonia delle sfere”, e specialmente le idee fondamentali di Keplero al riguardo, vengono confermate per la prima volta, e teoricamente questo puó essere verificato da tutti. Questa non è una autentica prova matematica, perché questa non puó essere data dal calcolo di probabilità. Nonostante ció, possiamo affermare, in altre parole, che nel nostro sistema solare ci deve essere stata una influenza, o una forza, che con una probabilità di almeno il 99,9% ha portato a una organizzazione delle velocità orbitali che corrisponde alle relazioni numeriche degli intervalli musicali-armonici..
Figura 1.2 Intervalli di velocità relativi a Mercurio ”in b” come chiave (=c), trasposti in una ottava.
Gli intervalli musicali sono contrassegnati da linee orizzontali. © Keplerstern Verlag
