La supposizione di una corrispondenza tra la geometria e le relazioni tra i corpi celesti è stata presente nell’umanità per un periodo altrettanto lungo quanto l’idea dell‘“armonia delle sfere“. Platone asssociò i cinque solidi regolari, che dopo lui furono chiamati solidi platonici, con gli elementi fuoco, acqua, terra, aria ed etere. Egli attribuì l’ultimo al dodecaedro, una figura che è formata da dodici pentagoni. Fu di nuovo Giovanni Keplero che 2000 anni dopo sviluppò questo approccio geometrico. Egli iniziò la sua ricerca di un ordine nel sistema solare creando il famoso modello che mostra l’organizzazione dei sei pianeti conosciuti al suo tempo in relazione ai cinque solidi platonici. Secondo questo modello, il rapporto dei raggi delle sfere interna ed esterna del dodecaedro, per esempio, corrisponde (sebbene molto approssimativamente) con quello della distanza media tra Marte e la Terra dal Sole, in altre parole il semi-asse maggiore dell’orbita ellittica.
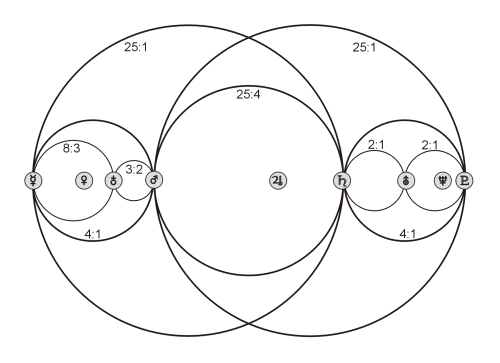
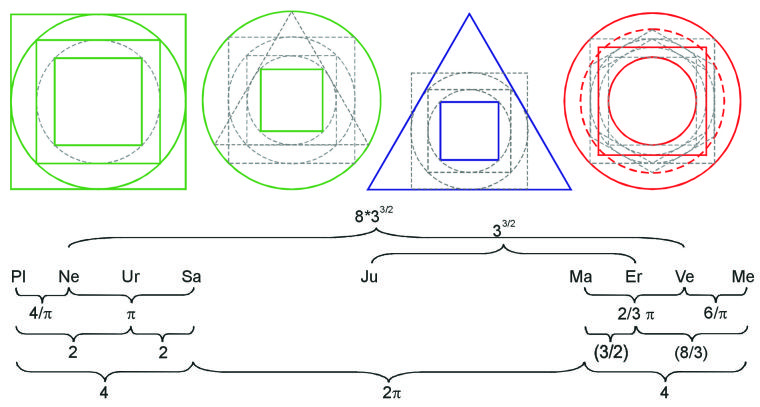
Comunque, la struttura dell’intero sistema, come spiegato nel libro Nel Segno delle Sfere celesti, è determinato dai semi-assi minori b, che hanno già avuto un’importanza centrale nell’armonia delle velocità. La cosa più sorprendente è che il primo e il quarto pianeta , contando iniziando dall’interno come dall’esterno, mostrano la proporzione di 4:1, relativa ai loro semi-assi minori. Il primo e il sesto pianeta, di nuovo contati dall’interno e dall’esterno, mostrano la proporzione di circa 25:1. Il risultato è una chiara struttura superiore, che è ulteriormente ripartita in rapporto a numeri piccoli interi. Questo ordine è illustrato nella prossima Figura 4.2 da cerchi. Le differenze dai valori reali ammontano a solo pochi millesimi, ad eccezione degli intervalli 8:3 e 3:2, dove sono leggermente superiori all’uno per cento (i valori esatti possono essere trovati in Nel Segno delle Sfere celesti, pag. 17).
© Keplerstern Verlag
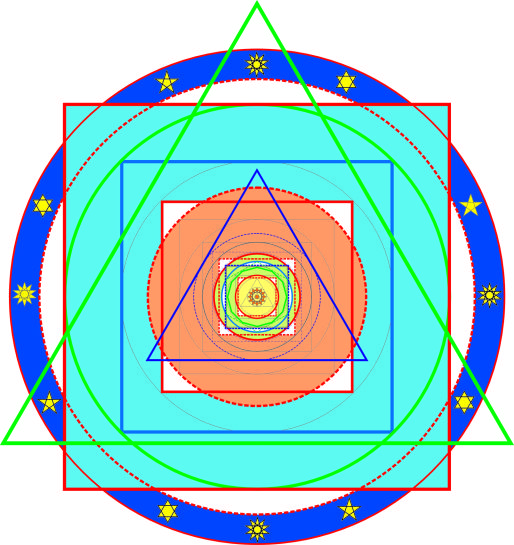
Cerchio: Nettuno
Quadrato intermedio: Urano
Quadrato interno: Saturno
L’organizzazione che si sviluppa è così chiara e semplice, che ci si meraviglia di nuovo, per il fatto che, almeno nella conoscenza dell’autore, non sia mai stato menzionato altrove. Quello che vediamo è qualcosa come un riflesso in Giove, il più grande tra i pianeti, anche se Venere e Nettuno non sono ancora integrati nell’ordine rappresentato. Raggiungiamo questo risultato usando le figure regolari più semplici: cerchio, quadrato e triangolo. Le proporzioni 2:1 e 4:1 possono essere derivate dai rapporti delle aree del cerchio interno e del cerchio esterno con un quadrangolo e un triangolo rispettivamente. Inoltre il rapporto dei cerchi con il quadrato è nella forma 4:pi, pi:2 ecc. (pi greco). Per esempio: otteniamo l’ordine seguente per i quattro pianeti esterni:
| Relazione planetaria |
Relazione geometrica |
Differenza (%) | |
|---|---|---|---|
| Ur/Sa | 2.012 | 2.000 | 0.608 |
| Ne/Ur | 1.568 | 1.571 | 0.156 |
| Pl/Ne | 1.271 | 1.273 | 0.181 |
| Pl/Sa | 4.011 | 4.000 | 0.270 |
Differenze tra gli intervalli planetari e le relazioni geometriche delle aree: valore medio 0,31%
Può sorprendere dapprima di trovare tre delle orbite come quadrangoli. Ciò a cui ci avviciniamo, comunque, è la rappresentazione del principio sottostante alle distanze, cioè i semi-assi minori. Questi rapporti sono uguali ai rapporti tra le aree dei quadrati o cerchi, rispettivamente. Ma perché i semi-assi minori giocano un ruolo decisivo nell’organizzazione delle orbite planetarie e perché le loro proporzioni devono essere determinate dai rapporti delle aree?
Una risposta può essere trovata nel fatto che i semi-assi minori costituiscono la metà geometrica delle distanze dell’afelio e del perielio, che li rendono i candidati ideali per un’organizzazione geometrica. Ora, se le misure delle distanze sono determinate dalle relazioni delle aree, le leggi di Keplero dicono – perlomeno per quanto riguarda la figura geometrica del cerchio – che le velocità corrispondono approssimativamente ai raggi, e i periodi di rivoluzione alle sfere costruite sui raggi.
Comunque, non si intende qui proporre una nuova teoria fisica, ma descrivere fenomeni degni di nota, poiché in questo modo possiamo esprimere geometricamente tutte le relazioni dei semi-assi minori (per il sistema planetario interno ci serve solamente l’esagono come strumento aggiuntivo).
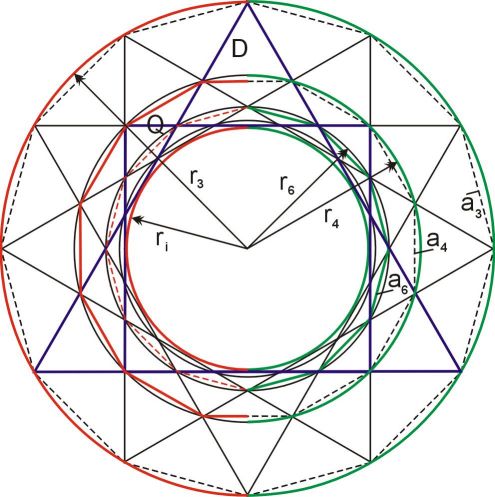
regione esterna, Saturno/Marte, Giove/Terra, regione interna. ©Keplerstern Verlag
Usando appropriati metodi statistici possiamo mostrare che la probabilità di una occorrenza casuale delle proporzioni che risultano da questi semplici principi di costruzione è molto piccola (< 1/100,000). Inoltre è possibile integrare il Sole (per mezzo del suo diametro) in questo tipo di rappresentazione. Ma il fatto più sorprendente è che troviamo tutte le proporzioni descritte esattamente nei rapporti delle aree, che appaiono nella stella a 12 punte.
Pertanto, l’idea di base di Giovanni Keplero di un ordine particolare nel nostro sistema solare viene elegantemente confermata, anche se in maniera modificata. L’intenzione più generale del suo “De Harmonice mundi” pubblicato nel 1619, era di sottolineare che la base della geometria, dell’armonia musicale e dell’astronomia sono essenzialmente una, o, in altre parole, le diverse sfere dell’esistenza sono intessute dagli stessi principi creativi. Gli archetipi geometrici, alla fine, sono per Keplero ciò che tiene assieme il mondo: pensieri divini, che sottostanno alla struttura della musica e del cosmo. Questi archetipi sono presenti anche nell’anima dell’uomo, rendendoci capaci di riconoscere l’armonia nelle diverse sfere dell’esistenza e di metterle in relazione.
Cerchio, quadrato e triangolo, quindi, sono i simboli invisibili inscritti nel cielo, che in modo così impressionante rappresentano l’ordine misterioso presente nel nostro sistema solare. Attraversando il mondo con occhi aperti scopriamo sempre di nuovo come queste tre figure si combinano in eloquente simbolismo. Gli esseri umani li collegano, nel pensiero delle scienze naturali, con l’idea di un ordine cosmico valido in generale e razionalmente comprensibile; sotto l’aspetto religioso, con la certezza della loro fede in una forza creativa che ha ordinato il mondo in modo che, alla fine, tutto andrà bene. La nostra dimora celeste porta queste tre figure geometriche archetipiche – unificate nel numero della perfezione – come un segno, quasi una segnatura, ma forse anche come una sfida e una promessa (Nel Segno delle Sfere celesti, versione inglese pag. 292).